Smooth Pycnophylactic Interpolation Produced by Density-Equalising Map Projectionshttps://doi.org/10.32909/kg.21.37.3

Abstract

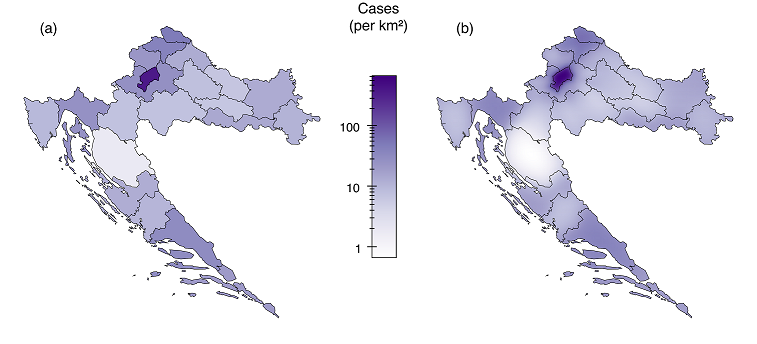
A large amount of quantitative geospatial data is collected and aggregated in discrete enumeration units (e.g. countries or states). Smooth pycnophylactic interpolation aims to find a smooth, nonnegative function such that the area integral over each enumeration unit is equal to the aggregated data. Conventionally, smooth pycnophylactic interpolation is achieved by a cellular automaton algorithm that converts a piecewise constant function into an approximately smooth function defined on a grid of coordinates on an equal-area map. An alternative approach, proposed by Tobler in 1976, is to construct a density-equalising map projection in which areas of enumeration units are proportional to the aggregated data. A pycnophylactic interpolation can be obtained from the Jacobian of this projection. Here, we describe a software implementation of this method. Although solutions are not necessarily optimal in terms of predefined quantitative measures of smoothness, our method is computationally efficient and can potentially be used in tandem with other methods to accelerate convergence towards an optimal solution.